kdb+ Database Setup Utilities
Data Intellect
This blog post describes tools to help setup a new kdb+ database. The tools allow you to:
- calculate the expected memory requirements of the database
- check columns have been typed correctly in order to avoid sym file bloat
Background
The volume of data that a kdb+ process can store in memory is finite and must be estimated and considered when designing a kdb+ system. The space required is easy to underestimate due to the kdb+ buddy memory allocation algorithm. It allocates memory in powers of two, meaning that the amount of memory required by a process to store a list of data is rounded up to the nearest power of two. This leads to miscalculations when creating databases as it is easy to underestimate the amount of memory required to store a table in memory. For example, consider a very simple example of a list of numbers:
q)// -22! Is an optimized shortcut to obtain the length of an
q)// uncompressed, serialized variable x
q)-22!10000000?10i
40000014
q)\ts 10000000?10i
273 67109136
q)// Calculating the allocated 2n size memory block from the first approximation
q)// gives a value similar to the memory reading from \ts
q)`long$2 xexp ceiling 2 xlog -22!10000000?10i
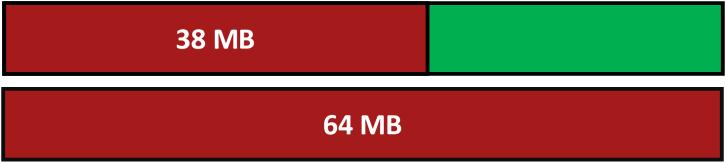
67108864In reality, what appears to take up 38MB actually takes up 64MB.
The calculation is complicated by more complex structures such as nested lists and lists with attributes. If we extend this example to a sample of a trades and quotes table:
q)\ts t:([]date:2017.01.01; size:600000?250; price:600000?100.; exch:600000?.Q.a)
19 22020832
q)-22!t
12600068
q)
q)//Further differential between estimated and real values when a `g# attribute is added
q)\ts t:([]date:2017.01.01; size:600000?250; price:600000?100.; exch:`g#600000?.Q.a)
27 28837888 A more detailed memory management blog post can be seen here.
Estimating Database Size
AquaQ’s dbestimate.q script seeks to address these issues, taking into account the additional overhead of these structures. It makes two assumptions:
- The number of distinct values in any column with a `g# attribute
- All untyped columns are strings of a fixed size
The `g# attribute has the largest memory overhead of all the attributes as it stores a lookup table with distinct values and the indexes at which those values appear. The lookup dictionary stored behind-the-scenes is similar to that returned by running group on a vector. We make an assumption for the number of distinct values, and we also assume that they are evenly distributed.
q)// Creating a list of sample syms
q)g:100?`a`b`c`d`e`f
q)// Grouping together: each value is an index of occurrence of the key
q)group g
c| 0 1 2 6 10 19 36 38 59 67 68 73 81 88 89
a| 3 9 12 14 18 23 27 37 42 46 49 52 53 58 60 63 71 82 96
f| 4 5 7 17 25 44 47 55 61 62 65 70 72 77 98
d| 8 15 16 21 28 32 34 41 45 48 54 74 85 86 87 92 93
b| 11 13 26 29 31 33 35 51 56 57 64 66 83 84 91 94
e| 20 22 24 30 39 40 43 50 69 75 76 78 79 80 90 95 97 99We make an assumption for the number of distinct values, and we also assume that they are evenly distributed.
The second assumption considers the way memory is allocated to nested columns in kdb+. We will assume all nested/untyped columns are strings. Strings are stored as lists of characters where each character is 1 byte in size. Each element of a nested column is stored as a list. A list has a fixed overhead of 16 bytes which means the minimum size of each element is 32 bytes. In addition, there is an 8 byte pointer for each element of the column. This means that nested columns usually require much more space than non-nested columns.
Better Estimation
First, we define two empty schemas in the format we expect the data to arrive. For this post, we define a quote and trade table and save it to a file called schema.q:
quote:([] time:`timestamp$(); `g#sym:`symbol$(); src:`symbol$(); bid:`float$(); ask:`float$(); bsize:`int$(); asize:`int$());
trade:([] time:`timestamp$(); `g#sym:`symbol$(); src:`symbol$(); price:`float$(); amount:`int$(); side:`symbol$());We then need to define roughly how many quotes and trades we are expecting per day and set values for the two assumptions stated above. We set a reasonable value for the number of distinct syms and the average length of string columns in the table to be 15 i.e. each string will occupy a 32 byte memory block plus an 8 byte pointer. From the schema defined above, we can see that all columns types are between 1 and 19h and there is a `g# attribute applied to the sym column to make queries that filter on the sym column run faster. We then call tablesize with the empty table and estimated row count.
We can see that estimating the size of a table isn’t a straightforward multiplication of row count by type size. For example, we’ll consider tables of 10 million quotes and 1 million trades with 10,000 distinct symbols per day, an average string length of 15 and a `g# attribute on the sym column. We’ll also include our table, t, defined above:
>q dbestimate.q -schema schema.q -distincts 10000 -avgsl 15
Loading schema for: trade
time sym src price amount side
------------------------------
Loading schema for: quote
time sym src bid ask bsize asize
--------------------------------
Loading schema for: t
date size price exch
--------------------
Assumptions:
Number of distinct values: 10000
Average string length: 15
Size per table in MB:
tbl | counts size
-----| -----------
trade| 600000 52
quote| 600000 56
t | 600000 28
Total size in MB:
136Avoiding Sym File Bloat
Symbol type values get enumerated when writing down to disk and a list of unique symbols are stored in the sym file. If a table has a large number of unique symbols per day this causes the sym file to grow very rapidly and become bloated which makes queries and enumeration operations run slower. In these circumstances, it is often better to save the column down as a string. Whilst this takes up more space, it prevents the sym file from becoming bloated which is a difficult problem to fix.
When a tick capture system is set up and a full days’ worth of data stored in the RDB, it makes sense to calculate the real ratio of distinct symbols to total records to ensure that the initial estimate of distinct symbols was correct. We can calculate this ratio using the ‘distinctratio’ function which can be found in our kdb-utilities repo. The date is the date for which we want to calculate values. A sample output of the function is shown below using randomly generated test data.
We can see from the table that in one day, there are 51316 distinct src values (around 10{e673f69332cd905c29729b47ae3366d39dce868d0ab3fb1859a79a424737f2bd} of the total column data).
q)// Sample quote data
q) quote:([] date:asc 1000000?(2016.12.30;2016.12.31); time:asc 1000000?00:00:00.000; sym:1000000#10000?`4; src:1000000#100000?`4; bid:1000000?100. + 1000?150.; ask:1000000?150. + 1000?100.; bsize:1000000?100+til 200; asize:1000000?100+ til 200)
q)// Distinct ratio calculation function
q)\l sfgrowth.q
q)distinctratio[2016.12.30]
counter distinctcount colname tab distinctpercent
-----------------------------------------------------------
500945 51316 src quote 10.24384
500945 9275 sym quote 1.851501This might be reasonable if the symbol set each day is highly repetitive. However, if the symbol universe were to increase by ~10{e673f69332cd905c29729b47ae3366d39dce868d0ab3fb1859a79a424737f2bd} each day, this would cause the sym file to become bloated and subsequently affect the efficiency of queries to the RDB. This is where sym file growth rate becomes important as it can affect database design choices. The following function calculates the symbol growth rate for all tables in the top level namespace over a specified date range and can also be found in our kdb-utilities repo.
q)\l sfgrowth.q
q)sfgrowth[2014.04.21;2014.04.25]
col date tab cnt total percent
--------------------------------------------
sym 2014.04.22 trades 5716 7551 75.69858
sym 2014.04.23 trades 7031 11478 61.25632
sym 2014.04.24 trades 4355 8875 49.07042
sym 2014.04.25 trades 4492 11225 40.01782
sym 2014.04.22 quotes 10018 106846 9.376111
sym 2014.04.23 quotes 2631 113865 2.310631
sym 2014.04.24 quotes 532 73071 0.728059
sym 2014.04.25 quotes 320 83844 0.3816612
src 2014.04.22 quotes 0 106846 0
src 2014.04.23 quotes 0 113865 0
src 2014.04.24 quotes 0 73071 0
src 2014.04.25 quotes 0 83844 0
src 2014.04.22 trades 0 7551 0
src 2014.04.23 trades 0 11478 0
src 2014.04.24 trades 0 8875 0
src 2014.04.25 trades 0 11225 0It should be noted that the function ignores the 1st day as all symbols would be considered new. We generate a dummy HDB containing trades and quotes tables. We can see from the output of the sfgrowth function that the sym column of the trades table grows by 75{e673f69332cd905c29729b47ae3366d39dce868d0ab3fb1859a79a424737f2bd} on day 1, then a further 61{e673f69332cd905c29729b47ae3366d39dce868d0ab3fb1859a79a424737f2bd}, 49{e673f69332cd905c29729b47ae3366d39dce868d0ab3fb1859a79a424737f2bd} and 40{e673f69332cd905c29729b47ae3366d39dce868d0ab3fb1859a79a424737f2bd} over the next 3 days. This is a prime example of the cause of sym file bloat. In contrast, the symbol list for the src column doesn’t grow at all after day 0.
Columns such as sym and src are generally not to blame for sym file bloat as the number of companies trading on an exchange does not fluctuate that much which means we can expect a high percentage of repetition each day. Symbol type columns containing a high ratio of distinct to total records, such as unique ID columns are more likely to be a problem. Such columns should be left untyped and processed as strings to avoid enumerating vast numbers of non-repetitive symbols.
Conclusion
Memory usage is a key issue in designing tick data capture systems in kdb+ as it can have significant side effects when not accurately estimated. This post highlights the importance of column type selection, attribute overheads, enumerated vs. string values and distinct value ratio as well as detailing the effects on the system and for the user.
There are other ways to minimize memory usage in a data capture system. Some data sets which are not required intraday do not have to be stored in-memory and can be written straight through to disk. This functionality is available in AquaQ’s TorQ framework.
Share this: